In geologia strutturale, l’analisi delle deformazioni osservate nelle rocce, sul terreno o al microscopio (strain analysis) consente di fare alcune assunzioni su quali siano stati gli sforzi che hanno provocato tali deformazioni (stress analysis).
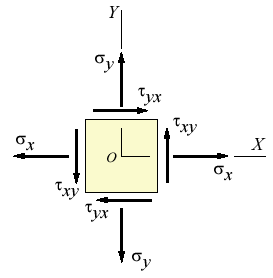
Nell’analisi dello stress è conveniente descrivere gli sforzi all’interno di un sistema di coordinate. In 2 dimensioni, uno sforzo σ ha componenti parallele agli assi x ed y, ossia σx e σy. Il relativo sforzo di taglio avrà una componente τxy (legata a σx e parallela all’asse y) ed una componente τyx (legata a σy e parallela all’asse x). Queste sono le 4 componenti dello stress piano (caso particolare in cui nessuno sforzo agisce perpendicolarmente al piano xy, cioè in direzione z).
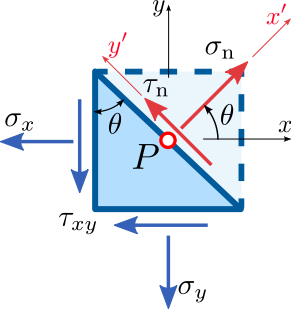
Componenti dello stress su un piano inclinato
Lo stress su di un piano orientato di un angolo θ rispetto all’asse y è rappresentato come nella figura in alto. Esiste un valore dell’angolo θ per cui si avrà il massimo valore di σ.
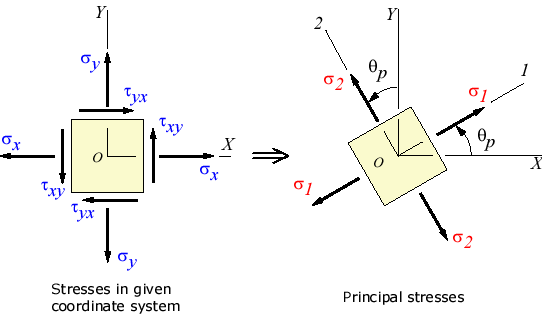
Nell’arco di 360° esistono 2 direzioni tra loro perpendicolari per cui si avranno un valore massimo ed uno minimo dello sforzo di taglio; gli sforzi perpendicolari a queste superfici sono detti stress principali σ1 e σ2. In queste due direzioni gli sforzi di taglio sono nulli.
Negli stati di stress tridimensionali, lo sforzo omogeneo può sempre essere analizzato in termini di 3 stress principali tra loro perpendicolari σ1 ≥ σ2 ≥ σ3, detti rispettivamente sforzo principale maggiore, intermedio e minore.
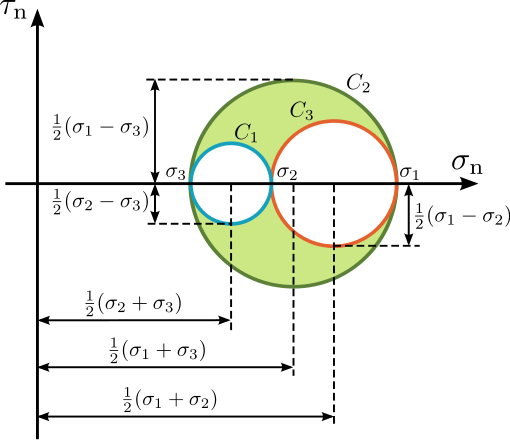
Il calcolo dello stress su una superficie la cui normale sia ad un angolo θ dallo stress principale maggiore σ1 può essere eseguito in un diagramma in cui σ sia l’asse x e τ l’asse y. Tutte le coppie di valori σ e τ che si hanno sui diversi piani al variare dell’angolo θ da 0 a 360° sono punti di una circonferenza detta Cerchio di Mohr.
Il cerchio interseca l’asse delle x ai valori σ1 e σ3; il suo raggio è (σ1 – σ3)/2; il suo centro è in (σ1 + σ3)/2 e corrisponde al valore di σ2.
I valori massimi e minimi di sforzo di taglio si trovano sempre su due piani allo stesso angolo (θ ± 45°) con l’asse di stress principale.
Alti valori dello sforzo di taglio sono legati a differenze di stress, non ai valori assoluti dello stress principale. In 3 dimensioni ciò accade su due superfici coniugate che si intersecano lungo l’asse di stress intermedio σ2 ad angoli di ± 45° con σ1 e σ3.
In situazioni diverse dallo stress piano, abbiamo componenti dello sforzo nella direzione dell’asse z. In totale si hanno 9 componenti del tensore degli sforzi, 3 delle quali sono normali ai piani cartesiani: σxx, σyy e σzz; Sui piano con sforzo di taglio pari a zero (τ = 0) essi diventano i piani di sforzo principali σ1, σ2 e σ3.
Sia lo sforzo che la deformazione sono “tensori di secondo ordine”. Uno scalare è un tensore di ordine zero (un solo valore, niente proprietà direzionali); un vettore è un tensore di primo ordine (grandezza e direzione). I tensori di secondo ordine definiscono le interazioni tra vettori ed operatori direzionali.
Esistono 3 piani perpendicolari tra loro su cui non agisce alcuno sforzo di taglio. Questo accade anche per la deformazione dove si parlerà di assi di deformazione principale.